密码学基础

加密分类

可逆和不可逆加密的应用场景并不相同所以无所谓优缺点，只能说是在相同的场景下加密算法的安全性的高低比较！

​

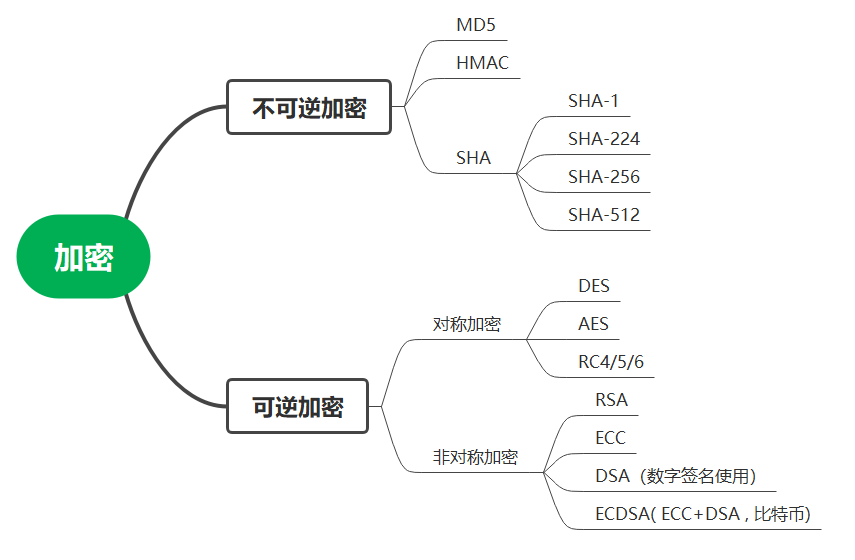
不可逆加密

不对称加密主要通过Hash函数来实现。常见的哈希函数包括 MD5、SHA-1、SHA-256 等。然而，由于演变的安全性和哈希碰撞问题，现在更常用的是安全性更高的哈希函数。

• 含义：单项加密，只能从明文经过算法到密文，而不能通过密文获得明文信息（不需要密钥）
• 应用场景：用户密码加密

可逆加密

含义：双向加密，明文密文可以通过加密解密过程得到（需要密钥）

对称加密

加密解密使用的同一个密钥

• 优点：加密和解密速度快，加密强度高，且算法公开

• 缺点：实现密钥的秘密分发困难，在大量用户的情况下密钥管理复杂，而且无法完成身份认证等功能

• 过程：

  • 双方约定一个密钥（规则）
  • 加密：原文 + 密钥 = 密文
  • 解密：密文 - 密钥 = 原文

• 欧拉公式

非对称加密

使用两把完全不同但又是完全匹配的一对钥匙（即一把公开密钥或加密密钥和专用密钥或解密密钥）——公钥和私钥

• 优点：非对称加密算法的保密性比较好，它消除了最终用户交换密钥的需要
• 缺点：加密和解密花费时间长、速度慢，不适合于对文件加密而只适用于对少量数据进行加密。
• 过程：
  • A —-> B， B将自己公钥发送
  • A加密：B公钥 + 原文 = 密文
  • B解密：密文 - B私钥 = 原文

MD5

MD5（Message Digest Algorithm 5）是一种哈希算法，用于将任意长度的消息转换为固定长度的哈希值（通常是128位）。由于不同的输入可能会生成相同的MD5值，加解密的场景一般需要使用更强大的算法，MD5一般用于文件校验。MD5算法经历以下步骤

• 数据填充
  填充消息使其长度与 448 模 512 同余（即长度 ≡ 448 mod 512）。填充的比特位格式为一个 1，后面跟着若干个 0

• 添加长度
  在第一步的结果之后附上 64 位的消息长度。此时，消息长度是512的整数倍

• 初始化变量

  使用四个 32 位的寄存器（A、B、C、D）来存储中间状态。这些寄存器初始值是固定的，并且在每次计算新的消息摘要时都会重新初始化。 A＝01234567h，B＝89abcdefh，C＝fedcba98h，D＝76543210h。

• 处理消息分组

  将填充后的消息分成多个 512 位的消息分组，并对每个消息分组进行处理。每个消息分组又被划分为 16 个 32 位字。MD5 算法采用分组密码结构，通过多轮迭代运算和位操作运算，对每个消息分组进行处理，生成中间哈希值。

• 迭代压缩

  MD5 算法使用四个基本的非线性函数（F、G、H、I）和四轮迭代运算对消息分组进行压缩。每轮迭代使用不同的函数和消息分组的子集，并在每轮迭代中更新寄存器的值。

• 输出结果

  在处理完所有消息分组后，将最终的寄存器值连接起来，得到最终的 128 位哈希值，即 MD5 摘要。

SHA

SHA 是一组由美国国家安全局（NSA）设计的安全哈希算法，用于生成消息摘要。SHA 算法有多个版本，包括 SHA-1、SHA-256、SHA-512 等，其中 SHA-256 和 SHA-512 是较为常用的。SHA 算法的工作原理类似于 MD5，但使用更复杂的算法和更长的输出长度，以提供更高的安全性。

SHA算法的整体步骤与MD5是一致的。SHA-512（Secure Hash Algorithm 512）是 SHA 算法的一种，它使用 64 位的字长和 80 轮迭代压缩，生成一个 512 位的哈希值。以下是 SHA-512 算法的计算步骤：

• 消息填充

  填充消息使其长度与 896 模 1024 同余（即长度 ≡ 896 mod 1024）。填充的比特位格式为一个 1，后面跟着若干个 0

• 添加长度
  在第一步的结果之后附上 128 位的消息长度。此时，消息长度是512的整数倍

• 初始化变量

  初始化 SHA-512 算法的内部状态，使用固定的初始值作为初始哈希值，这些初始值称为 SHA-512 的“魔数”。SHA-512 有 6 个辅助函数每一个函数输入为 3 个 64 位的输入。

• 处理消息

  将填充后的消息分成多个 1024 位的消息分组，并对每个消息分组进行处理。每个消息分组进行压缩操作，通过多轮迭代和位操作运算，更新 SHA-512 算法的内部状态，生成中间哈希值。

• 输出结果

  在处理完所有消息分组后，将最终的哈希值连接起来，得到 SHA-512 摘要。这个哈希值通常是一个 512 位的二进制字符串。

AES

AES（Advanced Encryption Standard）高级加密标准，是一种对称加密算法，用于保护敏感数据的安全性。它是目前应用最广泛的对称加密算法之一，被广泛用于数据加密、网络通信、存储加密等领域。

AES 算法使用相同的密钥来进行加密和解密，因此也被称为对称加密算法。它的设计目标是提供高度的安全性、性能和效率，适用于各种平台和应用场景。AES 算法使用固定长度的密钥（128 位、192 位或 256 位）对输入数据进行加密和解密，其中密钥长度决定了算法的安全性。

	密钥长度（32位比特字)	分组长度(32位比特字)	加密轮数
AES 128	4	4	10
AES 192	6	4	12
AES 256	8	4	14

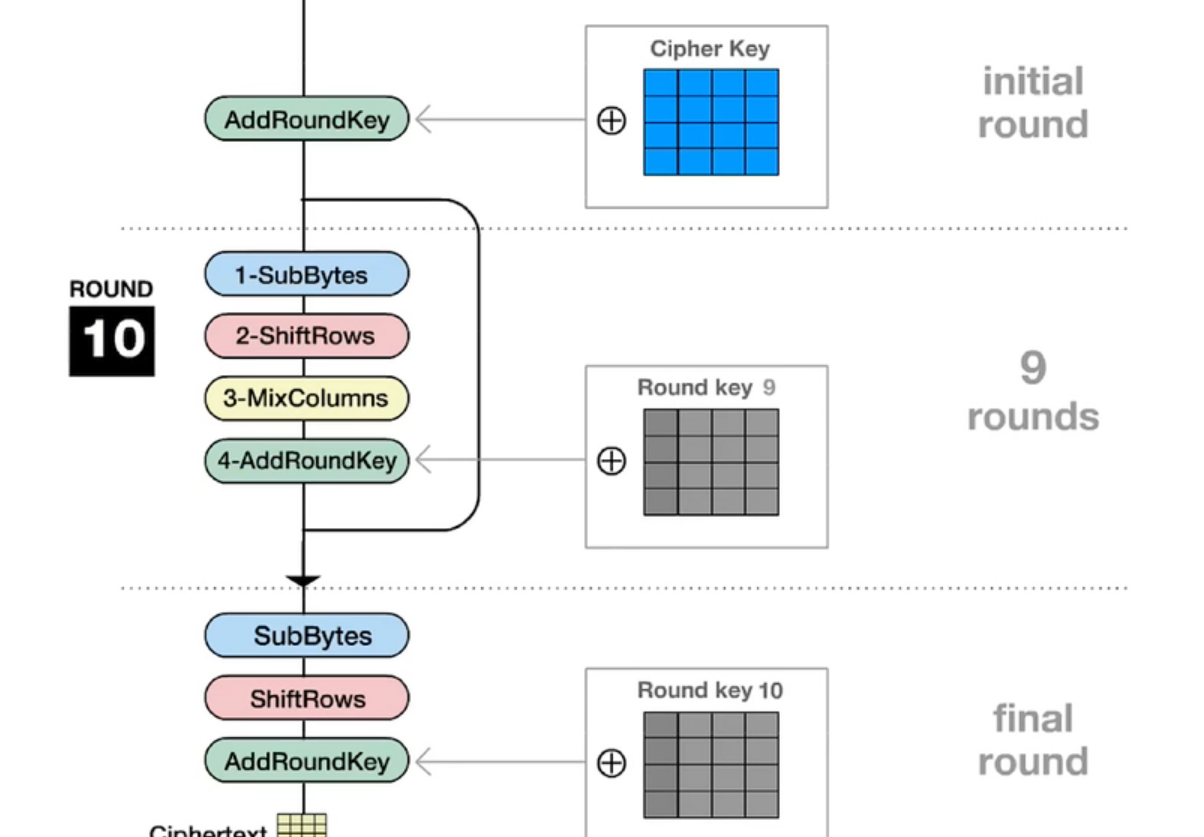
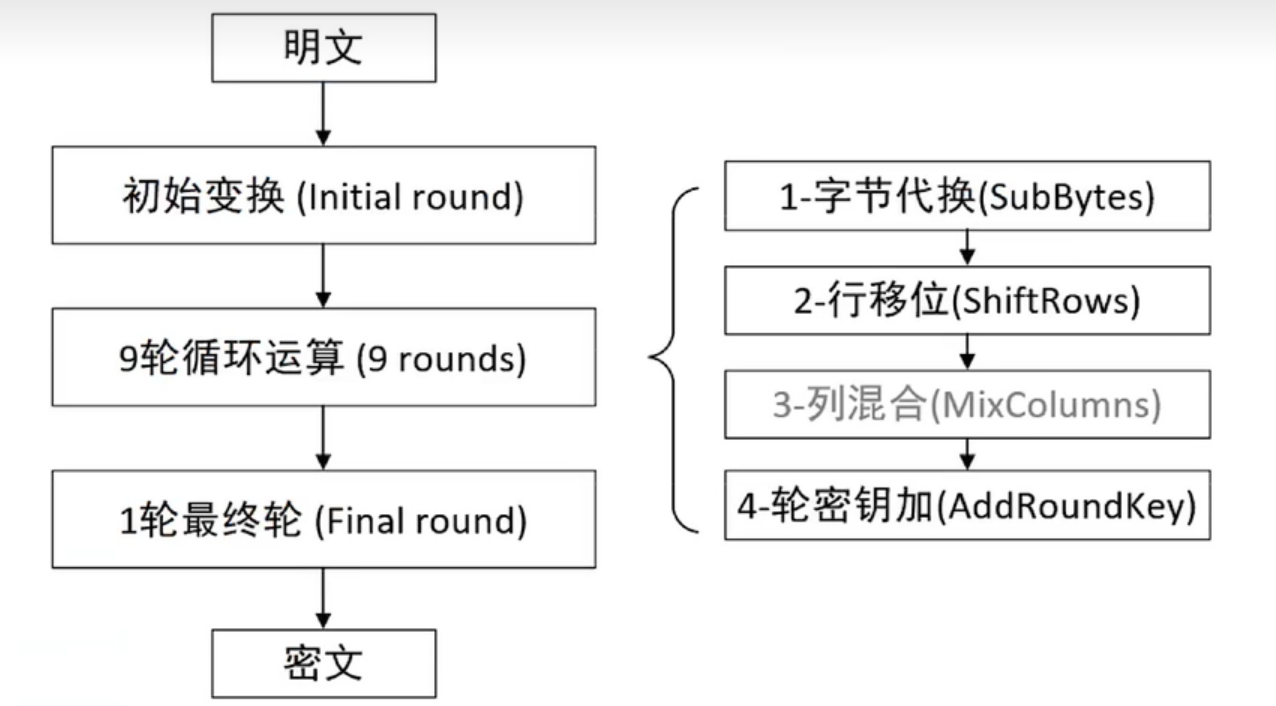
RSA

RSA（Rivest-Shamir-Adleman）是一种非对称加密算法，由 Ronald Rivest、Adi Shamir 和 Leonard Adleman 于 1977 年提出，并用他们三个名字的首字母来命名这个算法。它是目前应用最广泛的公钥加密算法之一，被广泛用于数据加密、数字签名、密钥交换等领域。

RSA 算法的核心思想是利用两个不相等的大素数及其乘积，构造公钥和私钥，其中公钥用于加密，私钥用于解密。RSA 算法的安全性基于大整数分解问题，即给定一个大合数，找到其质因数的乘积。目前尚未发现有效的、高效的算法来解决大整数分解问题，因此 RSA 算法在现代密码学中被认为是安全的。RSA是进行基本的数学运算，你要加密的消息越大，数字就越大，这就是为什么AES比RSA快。RSA的计算算法简要步骤如下：

1. 密钥生成：
   • 首先，选择两个不相等的大素数 p 和 q，并计算它们的乘积 n = p * q。n 称为模数（modulus）。
   • 计算欧拉函数 φ(n) = (p - 1) * (q - 1)。
   • 在区间 [1, φ(n)] 中选择一个整数 e，使得 e 和 φ(n) 互质（即它们的最大公约数为 1）。e 称为公钥（public key）的指数。
   • 计算整数 d，使得 (d * e) mod φ(n) = 1。d 称为私钥（private key）。
2. 加密：
   • 将明文 M 转换为整数 m，满足 0 <= m < n。
   • 计算密文 C = m^e mod n。
3. 解密：
   • 使用私钥 (d, n) 对密文 C 进行解密，计算明文 M = C^d mod n。

例子：

1. p = 61, q=53, n =p * q = 3233(110010100001)。
2. n一共有12位，所以这个密钥就是12位。实际应用中，RSA密钥一般是1024位，重要场合则为2048位。
3. φ(n) = (p - 1) * (q - 1) = 3120
4. 选择 e = 17。（实际应用中，常常选择65537）
5. d = 2753
6. n=3233，e=17，d=2753，所以公钥就是 (3233,17)，私钥就是（3233, 2753）。实际应用中，公钥和私钥的数据都采用ASN.1格式表达。
7. 假设发送的明文是65 ，加密C = 65 ^ 17 (mod 3233) =2790; 解密方根据密文解得M = C ^ 2753 (mod 3233)=65

参考资料

• Hash 算法（MD5、SHA-512)
• RSA + AES加密原理
• RSA算法原理（二）